Математическая закономерность. Математика в природе, нумерология в жизни

Введение. 2

Глава 1. Математические закономерности живой природы. 3

Глава 2. Принципы формообразования в природе 5

Глава 3. Золотое сечение 8

Глава 4. Геометрическая рапсодия Эшера. 15

Глава 5. Трансцендентное число   18

Список использованной литературы. 20

Введение.

При поверхностном знакомстве с математикой она может показаться непостижимым лабиринтом формул, числовых зависимостей и логических тропинок. Случайных посетителей, не познавших подлинной ценности математических сокровищ, страшит сухая схема математических абстракций, сквозь которую математик видит живое многоцветье реальности.

Тот же, кто постиг удивительный мир математики, не остаётся только восторженным созерцателем её сокровищ. Он сам стремится создавать новые математические объекты, ищет пути решения новых задач, или новые, более совершенные, решения уже решённых задач. Уже найдено и опубликовано более 300 доказательств теоремы Пифагора, десятки неклассических квадратур круга, трисекций угла и удвоений куба.

Но неспокойная пытливая мысль влечёт к новым поискам. При этом даже более чем сам результат привлекает поиск его. Это закономерно. Ведь путь к решению каждой достаточно содержательной задачи – всегда изумительная цепь умозаключений, сцементированная законом логики.

Математическое творчество – подлинное творчество ума. Вот что писал советский математик Г.Д.Суворов: «Теорема, записанная логически безупречно, действительно представляется лишённой какого-либо поэтического начала и кажется не плодом пламенной фантазии, а хмурым ребёнком мамы-логики. Но никто не знает, кроме учёного, какой вихрь фантазий и поэтических взлётов породил в действительности эту теорему. Ведь она была крылатой, экзотической бабочкой, прежде чем её пленили, усыпили логикой и прикололи к бумаге булавками доказательств! ». Закономерно, что в своих воспоминаниях К.Ф.Гаусс, А.Пуанкаре, Ж.Адамар, А.Н.Колмогоров и др. выдающиеся математики рассказали о великой радости, подлинном эстетическом наслаждении, которое они пережили, ища ответы на нерешённые задачи, которые для них были дорогами в незнаемое. Поскольку они шли к этим решениям впервые, и математика подарила им полную меру радости первооткрывателей.

В некоторых задачах среди многих дорог к ответу есть одна, самая неожиданная, часто тщательно «замаскированная» и, как правило, самая красивая и желанная. Большое счастье найти её и по ней пройти. Поиск таких решений, умение выйти за пределы возможностей уже известных алгоритмов является подлинной эстетической математического творчества.
^

Глава 1. Математические закономерности живой природы.

Живая природа демонстрирует многочисленные симметричные формы организмов. Во многих случаях симметричная форма организма дополняется красочной симметричной расцветкой.

Маленький, едва достигающий 4 мм берёзовый долгоносик, конечно же, не знает высшей математики. Но, изготовляя колыбельку для своего потомства, он «вычерчивает», вернее вырезает на листке дерева эволюту – кривую, представляющую собой множество центров кривизны листка. Сам же край листка будет эвольвентой по отношению к кривой, прорезаемой долгоносиком.

Сложным геометрическим закономерностям подчинена архитектура ячейки пчелиных сот.

Теоретические кривые и фазовая кривая колебаний численности популяций в совокупности двух взаимодействующих видов (биоценоза) «хищник-жертва».

Вито Вольтера (1860-1940) – выдающийся итальянский математик. Построил теорию динамики численности биологических популяций,

в которой применил метод дифференциальных уравнений.

Как и большинство математических моделей - биологических явлений, она исходит из многих упрощающих предположений.

В прыжках центр массы животных описывает хорошо известную фигуру - квадратную параболу, ветви которой обращены вниз: y=ax 2 , a>1, a

Красивы контуры листьев многих растений. С большой точностью формы их описываются изящными уравнениями в полярной или декартовой системе координат.

Глава 2. Принципы формообразования в природе

Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.

Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе.

Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.

Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».

Раковина моллюсков Nautilus, Haliotis и других формируются в форме логарифмической спирали:p=ae b φ .

Листья на молодых побегах растений располагаются по пространственной спирали. А рассматривая их сверху, обнаружим вторую спираль, поскольку они располагаются ещё так, чтобы не мешать друг другу воспринимать солнечный свет. Расстояния между отдельными листьями характеризуются числами ряда Фибоначчи: 1,1,2,3,5,8,…,u n , u n +1 ,…, где u n =u n -1 +u n -2.

В подсолнухе семечки расположены по характерным дугам, близким к двум семействам логарифмических спиралей.

Природа предпочла логарифмическую спираль благодаря многим замечательным свойствам этой кривой. Например, она не изменяется при преобразовании подобия.

Следовательно, организму нет надобности перестраивать архитектуру своего тела в процессе роста.

Ярким примером асимметрии живого на субмолекулярном уровне является вторичная форма материальных носителей наследственной информации - двойная спираль молекулы-гиганта ДНК. Но ДНК – уже спираль, накрученная на нуклеосому, она – спираль вдвойне. Жизнь возникает в трудноуловимом, поразительно точном процессе реализации планов природы-архитектора, согласно которым строятся молекулы белка.

Паук плетёт свою западню в форме сложной трансцендентной кривой – логарифмической спирали p=ae b φ

Глава 3. Золотое сечение

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

В математике пропорцией (лат. proportio) называют равенство двух отношений: a: b = c: d.

Отрезок прямой АВ можно разделить на две части следующими способами:

на две равные части – АВ: АС = АВ: ВС;
на две неравные части в любом отношении (такие части пропорции не образуют);
таким образом, когда АВ: АС = АС: ВС.

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

^ Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему

a: b = b: c или с: b = b: а.

Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC

Из точки В восстанавливается перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Свойства золотого сечения описываются уравнением:

x 2 – x – 1 = 0.

Решение этого уравнения:

Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.
^ История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

^ Динамические прямоугольники

Платон (427...347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет. «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».

Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д. Известен пропорциональный циркуль Дюрера.

Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».

^ Золотые пропорции в фигуре человека
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13: 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8: 5 = 1,6. У новорожденного пропорция составляет отношение 1: 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

^ Золотые пропорции в частях тела человека
В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.

Среди придорожных трав растет ничем не примечательное растение – цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.

Цикорий

Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

^ Ящерица живородящая

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.

Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.
^ Яйцо птицы

Великий Гете, поэт, естествоиспытатель и художник (он рисовал и писал акварелью), мечтал о создании единого учения о форме, образовании и преобразовании органических тел.

Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.

Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863...1925) считал золотое сечение одним из проявлений симметрии.

Глава 4. Геометрическая рапсодия Эшера.

Голландский художник Маур Корнелюс Эшер(1898-1971) создал целый мир зрительных образов, раскрывающих фундаментальные идеи и закономерности математики, физики, психологические особенности восприятия человеком объектов реальной действительности в окружающем нас трёхмерном пространстве.

Неограниченность пространства, зеркальные образы, противоречия между плоскостью и пространством - все эти понятия воплощены в запоминающихся, исполненных особого очарования образах. Ящерицы в наглядном виде представляют геометрические отображения, изучаемые в средней школе.

Всадники дают прекрасное наглядное представление о параллельном переносе, симметрии, заполнении всей плоскости фигурами сложной конфигурации.

«Куб и волшебные ленты». Ленты «Бельведер» - не просто -

действительно волшебные: геометрическая шутка, а целый

«протуберанцы» на них можно комплекс неожиданностей,

рас сматривать признак и выпуклости, порождённых особенностями и вогнутости. восприятия человеком предметов

Достаточно изменить точку зрения, в трёхмерном пространстве.

как ленты сразу перекрутятся
Мауриц Корнелюс Эшер создал уникальную галерею картин, принадлежащих одновременно искусству и науке. Они иллюстрируют теорию относительности Эйнштейна, строение материи, геометрические преобразования, топологию, кристаллографию, физику. Об этом свидетельствуют названия некоторых альбомов художника: «Неограниченное пространство», «Зеркальные образы», «Инверсии», «Многогранники», «Относительности», «Противоречия между плоскостью и пространством», «Невозможные конструкции».

«Я часто чувствую себя ближе к математикам, чем к своим коллегам-художникам», - писал Эшер. И действительно, его картины необычны, они наполнены глубоким философским смыслом, передают сложные математические отношения. Репродукции картин Эшера широко используются как иллюстрации в научных и научно-популярных книгах.

Глава 5. Трансцендентное число  

Природа числа  - одна из самых больших загадок математики. Интуиция подсказывала, что длина окружности и её диаметр – величины в равной степени постижимые.

Вычислением сотен десятичных знаков  на протяжении двух последних веков занимались многие ученые

В книге «Кошмары выдающихся личностей» известный английский математик и философ Бертран Рассел писал: «Лицо Пи было скрыто маской. Все понимали, что сорвать её, оставшись при этом в живых, не сможет никто. Сквозь прорези маски пронзительно, безжалостно, холодно и загадочно смотрели глаза». Может быть, для описания математического понятия излишне патетично, однако, в общем, верно. Действительно, история числа  - это волнующие страницы многовековой победной поступи математической мысли, неутомимого труда открывателей истины. Были на этом пути триумфы побед, были горькие поражения, драматические коллизии и комические недоразумения. Учёные проделали гигантскую работу поиска, раскрывая арифметическую природу одного из самых неподдающихся, загадочных и популярных чисел – числа, обозначаемого греческой буквой .

Шумеро-вавилонские математики вычисляли длину окружности и площадь круга с приближениями, которым соответствует значение =3, знали они и более точное приближение =3 1/8. В папирусе Райна (Ахмеса) указывается, что площадь круга равна (8/9*2R) 2 =256/81R 2

Это означает, что ≈3,1605… .
Архимед первым поставил задачу вычисления длины окружности и площади круга на научную основу. Итак, r =  > 48a 96 ≈3,1410>3 10/71

Учёный вычислил верхний предел (3 1/7): 3 10/71≈3,14084…Узбекский математик и астроном аль-Каши, работавший в научном центре известного математика и астронома Улугбека, вычислил число 2 с точностью до 16 правильных десятичных знаков: 2=6,283 185 307 179 5866.

С помощью удвоения числа сторон правильных, вписанных в окружность многоугольников он получил многоугольник с 800 355 168 сторонами.

Голландский математик Лудольф Ван Цейлен (1540-1610) вычислил 35 десятичных знаков  и завещал высечь это значение на своём могильном памятнике.

Одна из красивейших квадратур круга, выполненная польским математиком А.А.Коханьским (1631-1700).

Все построения выполняются при одном и том же растворе циркуля и быстро приводят к достаточно хорошему приближению числа.

Иоганн Генрих Ламберт (1728-1777) – немецкий математик, физик, астроном и философ. Сделал решающий шаг к разгадке числа . В1766г.

он доказал иррациональность числа . Итог раскрытию тайны числа  подвёл немецкийматематик Фердинанд Линдеман (1852-1939).

В 1882г. он доказал, что число  является трансцендентным. Тем самым была доказана невозможность квадратуры круга в классической постановке этой задачи.

Случайные события: они реализовались с помощью бросания иголки и также помогали учёным вычислить число  с достаточно высокой точностью.
Эту задачу впервые поставил и осуществил французский естествоиспытатель Жорж Луи Леклерк Бюффон(1707-1788).

Таким самым способом швейцарский астроном и математик Рудольф Вольф (1816-1896)в результате 5 тысяч бросаний иголки нашёл, что =3,1596.

Другие учёные получили следующие результаты: при 3204 бросаниях =3,1533; при 3408 бросаниях =3,141593.

Список использованной литературы.

1. Энциклопедический словарь юного математика

2. Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые.- М.: Наука, 1976

3. Маркушевич А.И. Замечательные кривые. – М., Наука, 1978

4. Стройк Д.Я. Краткий очерк истории математики. – М., Наука, 1984

5. Глейзер Г.И. История математики в школе., М., Просвещение, 1982

6. Гарднер М. Математические чудеса и тайны. М., Мир. 1978

Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
Кеплер И. О шестиугольных снежинках. – М., 1982.
Дюрер А. Дневники, письма, трактаты – Л., М., 1957.
Цеков-Карандаш Ц. О втором золотом сечении. – София, 1983.
Стахов А. Коды золотой пропорции.

Порой кажется, что наш мир прост и понятен. На самом деле это великая загадка Вселенной, сотворившей такую совершенную планету. А может, её создал тот, кто наверняка знает, что делает? Над этим вопросом трудятся величайшие умы современности.

Они каждый раз приходят к выводу, что невозможно сотворить все то, что мы имеем, без Высшего разума. Какая необыкновенная, сложная и в то же время простая и непосредственная наша планета Земля! Окружающий мир удивителен своими правилами, формами, красками.

Законы природы

Первое, на что можно обратить внимание на нашей огромной и удивительной планете, - это Она обнаруживается во всех формах окружающего мира, а также является основным принципом красоты, идеальности и пропорциональности. Это не что иное, как математика в природе.

Понятие "симметрия" означает гармонию, правильность. Это свойство окружающей действительности, систематизирующее фрагменты и превращающее их в единое целое. Ещё в древней Греции начали впервые замечать признаки этого закона. Например, Платон считал, что красота появляется исключительно вследствие симметрии и соразмерности. В действительности, если посмотреть на предметы пропорциональные, правильные и завершённые, то наше внутреннее состояние будет прекрасным.

Законы математики в живой и неживой природе

Давайте взглянем на любое существо, например самое совершенное - человека. Мы увидим строение тела, которое с обеих сторон выглядит одинаково. Ещё можно перечислять множество образцов, таких как насекомые, животные, морские обитатели, птицы. Каждый вид имеет свой окрас.

Если присутствует какой-нибудь узор или рисунок, он, как известно, отражается зеркально относительно центровой линии. Все организмы созданы благодаря правилам мироздания. Такие математические закономерности прослеживаются и в неживой природе.

Если обращать внимание на все явления, такие как смерч, радуга, растения, снежинки, то можно обнаружить в них много общего. Относительно листок дерева делится пополам, и каждая часть будет отражением предыдущей.

Еще если взять в качестве примера смерч, который возвышается вертикально и имеет вид воронки, то его тоже можно условно разделить на две абсолютно одинаковые половинки. Можно встретить явление симметрии в смене дня и ночи, времён года. Законы окружающего мира - это математика в природе, которая имеет свою совершенную систему. На неё опирается вся концепция создания Вселенной.

Радуга

Мы нечасто задумываемся над явлениями природы. Пошёл снег или дождь, выглянуло солнышко или грянул гром - привычное состояние меняющейся погоды. Рассмотрим разноцветную дугу, которую обычно можно обнаружить после выпадения осадков. Радуга в небе - удивительное явление природы, сопровождающееся видимым только человеческому глазу спектром всех цветов. Это случается за счёт прохождения лучей солнца через уходящую тучу. Каждая дождинка служит призмой, которая обладает оптическими свойствами. Можно сказать, что любая капля является маленькой радугой.

Проходя через водную преграду, лучи меняют свой изначальный цвет. Всякий поток света имеет определённую длину и оттенок. Поэтому наш глаз воспринимает радугу именно такой разноцветной. Заметим интересный факт, что это явление может лицезреть исключительно только человек. Потому что это всего лишь иллюзия.

Виды радуги

Радуга, образовавшаяся от солнца, встречается наиболее часто. Она является самой яркой из всех разновидностей. Состоит из семи основных цветов: красного оранжевого, жёлтого, зелёного, голубого, синего, фиолетового. Но если разобрать в подробностях, оттенков намного больше, чем наш глаз может увидеть.
Радуга, созданная луной, встречается в тёмное время суток. Считается, что её можно лицезреть всегда. Но, как показывает практика, в основном такое явление наблюдается только в дождливых местностях или около больших водопадов. Цвета лунной радуги очень тусклые. Их суждено рассмотреть лишь с помощью специальной техники. Но даже с ней наш глаз способен разобрать только полоску белого цвета.
Радуга, появившаяся вследствие тумана, подобна широкой сияющей светлой арке. Иногда этот вид путают с предыдущим. Сверху цвет может быть оранжевым, снизу - иметь оттенок фиолетового. Солнечные лучи, проходя сквозь туман, образуют прекрасное явление природы.
в небе возникает крайне редко. Она не схожа с предыдущими видами своей горизонтальной формой. явление можно только над перистыми облаками. Они, как правило, простираются на высоте 8-10 километров. Угол, под которым радуга покажет себя во всей красе, должен быть более 58 градусов. Цвета обычно остаются такими же, как в солнечной радуге.

Золотая пропорция (1,618)

Идеальную соразмерность чаще всего можно встретить в мире животных. Они награждены такой пропорцией, которая равна корню от соответствия числа PHI к единице. Это соотношение является связующим фактом всех животных на планете. Великие умы древности называли это число божественной пропорцией. Её ещё можно назвать золотым сечением.

Этому правилу полностью соответствует гармоничность строения человека. Например, если определить расстояние между глазами и бровями, то оно будет равно божественной постоянной.

Золотое сечение - это пример того, сколь важна математика в природе, закону которой начали следовать дизайнеры, художники, архитекторы, создатели красивых и совершенных вещей. Они создают с помощью божественной постоянной свои творения, которые имеют сбалансированность, гармонию и на них приятно смотреть. Наш ум способен считать красивым те вещи, предметы, явления, где есть неравное соотношение частей. Пропорциональностью наш мозг называет именно золотое сечение.

Спираль ДНК

Как справедливо отметил немецкий учёный Гуго Вейль, корни симметрии пришли через математику. Многие отмечали совершенность геометрических фигур и обращали на них внимание. Например, пчелиные соты - это не что иное, как шестиугольник, сотворённый самой природой. Ещё можно обратить внимание на шишки ели, которые имеют цилиндрическую форму. Также в окружающем мире часто встречается спираль: рога крупного и мелкого скота, раковины моллюсков, молекулы ДНК.

Сотворена по принципу золотого сечения. Она является связующим звеном между схемой материального тела и её реальным образом. А если рассмотреть мозг, то он представляет собой не что иное, как проводник между телом и разумом. Интеллект связывает жизнь и форму её проявления и позволяет жизни, заключённой в форме, познавать саму себя. С помощью этого человечеству достижимо понять окружающую планету, искать в ней закономерности, которые затем применять к изучению внутреннего мира.

Деление в природе

Митоз клетки состоит из четырёх фаз:

Профаза . В ней увеличивается ядро. Проявляются хромосомы, которые начинают закручиваться в спираль и превращаться в свой обыкновенный вид. Формируется место для деления клетки. В конце фазы растворяется ядро и его оболочка, и хромосомы вытекают в цитоплазму. Это самый продолжительный этап деления.
Метафаза . Здесь заканчивается закручивание в спираль хромосом, они образуют метафазную пластинку. Хроматиды располагаются противоположно друг другу, готовясь к делению. Между ними появляется место для рассоединения - веретено. На этом второй этап заканчивается.

Анафаза . Хроматиды расходятся в противоположные стороны. Теперь в клетке имеется два набора хромосом за счёт их деления. Этот этап очень короткий.
Телофаза . В каждой половинке клетки образуется ядро, внутри которого формируется ядрышко. Активно рассоединяется цитоплазма. Веретено постепенно исчезает.

Значение митоза

За счёт уникального способа деления, каждая последующая после размножения клетка имеет такой же состав генов, как её материнская. Состав хромосом обе клетки получают одинаковый. Здесь не обошлось без такой науки, как геометрия. Прогрессия в митозе имеет важное значение, так как по этому принципу размножаются все клетки.

Откуда берутся мутации

Этот процесс служит гарантией постоянного набора хромосом и генетических материалов в каждой клетке. За счёт митоза происходит развитие организма, размножение, регенерация. В случае нарушения из-за действия каких-то ядов хромосомы могут не разойтись по своим половинкам, или в них, возможно, будут наблюдаться нарушения в строении. Это станет явным показателем начинающихся мутаций.

Подводя итоги

Что общего в математике и природе? На этот вопрос вы найдёте ответ в нашей статье. А если копнуть глубже, то нужно сказать, что с помощью изучения окружающего мира человек познаёт самого себя. Без породившего все живое, не могло бы ничего быть. Природа находится исключительно в гармонии, в строгой последовательности своих законов. А возможно ли все это без разума?

Приведём высказывание учёного, философа, математика и физика Анри Пуанкаре, который, как никто другой, сможет дать ответ на вопрос о том, действительно ли математика в природе является основополагающей. Некоторым материалистам могут не понравиться такие рассуждения, но навряд ли они смогли бы их опровергнуть. Пуанкаре говорит, что гармония, которую человеческий разум хочет открыть в природе, не может существовать вне его. которая присутствует в умах хотя бы нескольких индивидов, может быть доступна всему человечеству. Связь, которая собирает воедино мыслительную деятельность, и называется гармонией мира. В последнее время на пути к такому процессу есть колоссальные продвижения, но они очень малы. Эти звенья, связывающие Вселенную и индивида, должны быть ценны любым человеческим умом, который чувствителен к этим процессам.

Понятие о гармонии. Математические закономерности композиции

Основы композиции в прикладной графике

Еще в глубокой древности человеком было обнаружено, что все явления в природе связаны друг с другом, что все пребывает в непрерывном движении, изменении, и, будучи выражено числом, обнаруживает удивительные закономерности.

В Древней Греции эпохи классики возник ряд учений о гармонии. Из них наиболее глубокий след в мировой культуре оставило Пифагорейское учение. Последователи Пифагора представляли мир, вселенную, космос, природу и человека как единое целое, где все взаимосвязано и находится в гармонических отношениях. Гармония здесь выступает как начало порядка - упорядочивания хаоса. Гармония присуща природе и искусству: "Одни и те же законы существуют для музыкальных ладов и планет ". Пифагорейцы и их последователи всему сущему в мире искали числовое выражение. Ими было обнаружено; что математические пропорции лежат в основе музыки (отношение длины струны к высоте тона, отношения между интервалами, соотношение звуков в аккордах, дающих гармоническое звучание). Пифагорейцы пытались математически обосновать идею единства мира, утверждали, что а основе мироздания лежат симметричные геометрические формы. Пифагорейцы искали математическое обоснование красоте. Они исследовали пропорции человеческого тела и утвердили математический канон красоты, по которому скульптор Поликлет создал статую "Канон".

Все классическое искусство Греции носит печать пифагорейского учения о про порциях. Его влияние испытали на себе ученые средневаковья, наука и искусство эпохи Возрождения, Нового времени вплоть до наших дней. Вслед за пифагорейцами средневековый ученый Августин назвал красоту "числовым равенством". Философ-схоласт Бонавентура писал: "Красоты и наслаждения нет без пропорциональности, пропорциональность же прежде всего существует в числах. Необходимо, чтобы все поддавалось счислению". Об использовании пропорции в искусстве Леонардо да Винчи писал в своем трактате о живописи: "Живописец воплощает в форме пропорции те же таящиеся в природе закономерности, которые в форме числового закона по знает ученый ".

Таким образом, пропорциональность, соразмерность частей целого является важнейшим условием гармонии целого и может быть выражена математически посредством пропорций.

Пропорция означает равенство двух или нескольких отношений. Существует несколько видов пропорциональности:

математическая,
гармоническая,
геометрическая и др.

В математической равенство двух отношений выражается формулой a:b=с:d , и каждый член ее может быть определен через остальные три. В гармонической пропорции - 3 элемента. Они являются или попарными разностями некоторой тройки элементов, или самими этими элементами, например:

а:с=(а - в): (в - с)

В геометрической пропорции тоже всего 3 элемента, но один из них общий, а:в=в:с . Разновидностью геометрической пропорции является пропорция так называемого "золотого сечения ", имеющая всего два члена - "а " и "в " - излюбленная пропорция художников, которую в эпоху Возрождения называли "божественной пропорцией".

Золотое сечение (з. с.)

Особенностью пропорции золотого сечения является то, что в ней последний член представляет собой разность между двумя предыдущими членами, т. е.

а:в=в: (а -в)

Отношение з. с. выражается числом 0,618 .
Пропорция з. с. 1:0,618=0,618:0,382 .

Если отрезок прямой выразить через единицу, а затем разделить его на два отрезка по з. с., то больший отрезок будет равен 0,618, а меньший 0,382.

рис 2. Деление отрезка по золотому сечению

На основании пропорции з. с. был построен ряд чисел, замечательный тем, что каждое последующее число оказывалось равным сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 1З, 21 и т. д. Этот ряд был открыт итальянским математиком Фибоначчи и называется поэтому рядом Фибоначчи. Он обладает тем свойством что, отношения между соседними членами по мере возрастания чисел ряда, все более приближаются к О,б18, то есть, к отношению з. с.

Пропорции з. с. ученые связывают с развитием органической материи. з. с. было обнаружено в объектах живой природы - в строении раковин, дерева, в расположении семян подсолнуха, в строении тела человека, а также его наблюдали в устройстве вселен ной в расположении планет.

В отношении з. с. находятся так же элементы геометрических фигур - пятиугольника, звезды.

В прямоугольнике з. с. стороны находятся в отношении з.с. Этот прямоугольник содержит в себе квадрат и малый прямоугольник з. с. (его большая сторона является малой стороной первоначального прямоугольника.) Поэтому можно построить пр-к з.с. на основании квадрата: сторона квадрата делится пополам, из той точки к вершине проводится диагональ, с помощью которой на стороне квадрата строится пр-к з.с.

Точки пересечения линий, составляющихзвезду, делят их на отрезки в отношении золотого сечения. Этот малый прямоугольник подобен большому прямоугольник, составленному из квадрата и малого прямоугольника з. с., то есть оба эти прямоугольника являются прямоугольниками з. с.

Иначе говоря, если отсечь от прямоугольника з. с.. квадрат, то остается меньший прямоугольник, стороны которого опять же будут находиться в отношении з. с. Разбивая этот меньший прямоугольник на квадрат и еще меньший прямоугольник, мы опять получим прямоугольник з. с., и так до бесконечности. Если соединить вершины квадратов кривой, то мы получим логарифмическую кривую, бесконечно растущую спираль, которую называют "кривая развития", "спираль жизни", ибо в ней как бы заложена идея бесконечного развития.

Рис. 4. Прямоугольник приблизительно золотого сечения, построенный на основании пятиугольника

Рис.5.Построение прямоугольника золотого сечения на основе квадрата.

Бесконечное повторение з. с. и квадрата при рассечении прямоугольника з. с. обнаруживает повторение целого в его частях, что является одним из условий гармонии целого. Это свойство прямоугольника з.с. было обнаружено художниками и они стали употреблять з. с. как способ гармонизации, способ пропорционирования. Фидий использовал з. с. при постройке Акрополя (5 век до н. э.)

Рис. 6.Логарифмияеская кривая "Спираль Жизни"

Рис. 7. Построение буквы из книги Луки Пачоли "О божественной пропорции"

Греческие ремесленники, создавая гончарные изделия также применяли з. с. В эпоху Возрождения з. с. использовали не только в зодчестве, скульптуре, живописи, но и в поэзии и музыке. Дюрер, Леонардо да Винчи и его ученик Лука Пачоли применяли з. с. в поисках гармоничных пропорций букв. Прямоугольник з. с. мы встречаем и в пропорциях средневековых рукописных книг, и в современной книге, так как стройные пропорции з. с. позволяют красиво организовать пространство книжной страницы и разворота.

Рис. 8. Схема идеальных пропорций средневековой рукописи.

Пропорции страницы 2:3, а плоскость, занятая письмом в пропорции золотого сечения.

Рис. 9. Один из способов определения рзмера полосы набора при заданном формате.

Пропорционирование - приведение частей целого к единому пропорциональному строю.

В ХХ веке вновь возродился интерес к золотому сечению как к способу пропорционирования.

Оно привлекло внимание архитекторов. Советский архитектор Жолтовский и француз Корбюзье занимались проблемами з. с. и использовали его в своей архитектурной практике, Корбюзье создал целую систему пропорционирования на основе чисел ряда золотого сечения и пропорций человеческого тела и назвал ее "Модулор", что по-латыни означает "ритмически размерять".

Рис. 9. Модулор (упрощенная схема)

Рис. 10. Варианты деления прямаугольника на основе Модулора.

Модулор Корбюзье представляет собой гармонические ряды чисел, которые связаны в единую систему и предназначены для использования в архитектуре и дизайне - для гармонизации всей среды, в которой обитает человек. Корбюзье мечтал о перестройке с помощью Модулора всей архитектурной и предметной среды. Сам он создал несколько прекрасных образцов архитектуры, но о более широком применении Модулора в существующих условиях не могло быть и речи.

Модулор использовался в ряде слуйаев в дизайне и в графическом дизайне - при конструировании печатных изданий. На рис. 16 приводятся варианты деления прямоугольника 3:4, приведенные Корбюзье для демонстрации возможностей конструирования с помощью Модулора.

В разработку вопроса пропорционирования и использования золотого сечения нес свой вклад Д.Хэмбидж. В 20-м году в Нью-Йорке вышла его книга "Элементы динамической симметрии". Хэмбидж исследовал динамическую симметрию, которую он обнаружил в ряде прямоугольников, с целью ее практического применения художниками в композиционном построении. Он делает попытку раскрыть секреты, которыми пользовались древние греки, добиваясь гармонического решения формы. Его внимание привлекли свойства прямоугольников, составляющих ряд, где каждый последующий прямоугольник строится на диагонали предыдущего, начиная с диагонали квадрата Ц2. Это прямоугольники Ц4, Ц5 (с меньшей стороной равной стороне квадрата, принятой за единицу). (Рис. 17). Кульминацией ряда является прямоугольник Ц5, обладающий особыми гармоническими свойствами и "родственный" прямоугольнику золотого сечения, (о нем будет сказано ниже).

Рис. 11. Ряд динамических прямоугольников Хэмбиджа.

Хэмбидж рассматривает также площади квадратов, построенных на сторонах этих прямоугольников и обнаруживает следующую динамику: в пр-ке Ц2 квадрат, построенный на большей стороне, имеет площадь в 2 раза большую, чем квадрат, построенный на меньшей стороне. В пр-ке Ц3 квадрат на большей стороне в 3 раза больше квадрата на меньшей стороне и так далее. Таким образом образуются динамические ряды площадей, состоящие из целых чисел.

Хэмбидж утверждает, что древние греки использовали этот принцип в своих композиционных решениях. Прямоугольники динамического ряда, о котором мы говорили, являются первичными площадями в композиционной системе Хэмбиджа. Каждый из этих прямоугольников может быть разбит на отдельные части и порождать новые композиционные решения, новые темы. Например, прямоугольник Ц5 можно разбить на квадрат и два прямоугольника золотого сечения. Прямоугольник золотого сечения может быть разбит на квадрат и прямоугольник золотого сечения, а также может быть разбит на равные части, при этом обнаруживается следующая закономерность: при делении пополам он даст два прямоугольника, в каждом из которых будет по два прямоугольника золотого сечения. При делении на три части - по три прямоугольника золотого сечения в каждой трети. При делении на 4 части - по четыре прямоугольника з. с. в каждой четверти основного прямоугольника.

Среди систем пропорционирования, используемых в архитектуре, дизайне, в прикладной графике следует упомянуть системы "предпочтительных чисел" и различные модульные системы.

"Предпочтительные числа " - ряд чисел геометрической прогрессии, где каждое последующее число образуется умножением предыдущего числа на какую-нибудь постоянную величину. Числа из предпочтительных рядов используются при конструировании упаковок, в композиции рекламных плакатов. Они обеспечивают ритмическое развитие формы, их можно встретить и в построении формы античной вазы и в современной станке.

Известна система пропорционирования - так называемые "итальянские ряды ", в основе которых лежат первые числа ряда Фибоначчи - 2, 3, 5. Каждое из этих чисел, удваиваясь, составляет ряд чисел, гармонически связанных между собой:

2 - 4, 8, 16, 32, 64, и т. д.
3 - 6, 12, 24 48, 96
5 - 10, 20, 40, 80, 160

Пропорционирование связано с понятиями соразмерности и меры . Одним из способов соизмерения целого и его частей является модуль. Модуль - размер или элемент, повторяющийся неоднократно в целом и его частях. Модуль (лат.) означает - мера. Любая мера длины может являться модулем. При строительстве греческих храмов, чтобы добиться соразмерности использовали также и модуль. Модулем мог служить радиус или диаметр колонны, расстояние между колоннами.

Витрувий, римский зодчий 1 в. до н. э., в своем трактате об архитектуре писал, что пропорция есть соответствие между членами всего произведения и его целым - по отношению к части, принятой за исходную, на чем и основана вся соразмерность, и соразмерность есть строгая гармония отдельных частей самого сооружения и соответсхвие отдельных частей и всего целого одной определенной части, принятой за исходную.

В прикладной графике модуль широко ислользуется при конструировании книг, журналов, газет, каталогов, проспектов, всяческих печатных изданий. Применение модульных сеток помогает упорядочить расположение текстов и иллюстраций, споеобствует созданию композиционного единства. В основе модульного конструирования печатных изданий лежит комбинация вертикальных и горизонтальных линий, образующих сетку, делящих лист (страницу) на прямоугольники, предназначенные для распределения текста, иллюстраций и пробелов между ними. Этот прямоугольный модуль (их может быть несколько) определяет ритмически организованное распределение материала в печатном издании.

Существуют сетки различного рисунка и степени сложности. А. Херлберт приводит в своей книге "Сетка" образцы модульных сеток для журналов, книг, газет.

Не следует путать модульную сетку с типографской сеткой, определяющей размеры полей и формат полосы набора. Конечно, модульная сетка, постольку, поскольку имеет дело с печатными изданиями, должна учитывать размеры строк, высоту литер, пробельные элементы в типографских мерах (квадраты, цицеро, пункты), чтобы правильно располагать печатный материал на странице.

Система сеток благодаря четкой модульной основе позволяет ввести в процесс проектирования издания электронные программы. В прикладной, промышленной графике модульную сетку применяют при конструировании всевозможных рекламных издании и, в особенности при проектировании графического фирменного стиля. Модульную сетку применяют при конструировании различных знаков, знаков визуальных коммуникаций, товарных знаков и др.

Рис. 14. Товарный знак, построенный на основе модульной сетки.

Рис. 15. Коммуникационный знак для Олимпийских игр в Мюнхене. построенный на модульной сетке

В основу модульных сеток часто бывает положен квадрат. Квадрат очень удобный модуль. Он широко используется как модуль в современной мебельной промышленноети, в собенности, при конструировании сборной мебели, "стенок".

Двойной квадрат издавна известен как модуль традиционного японского дома, где размеры комнат находились в соответствии с тем, сколько раз уложится на полу циновка-татами имеющая пропорции двойного квадрата.

В прикладной графике квадрат используется для форматов проспектов альбомов, детских книг, но он также определяет и внутреннее пространство этих изданий. Квадратный модуль может использоваться и не в квадратном формате.

Приведем пример использования квадратного модуля в квадратном формате: при трехколоночном наборе текста вся площадь, отведенная под текст и иллюстрации делится на 9 квадратов. Если ширину колонки обозначить 1, то квадрат будет 1х1. Иллюстрации при этом могут занимать площади: 1х1, 1х2, 1хЗ, 2х2, 2хЗ, ЗхЗ, 2х1, и т. д., то есть мы будем иметь достаточно широкие возможности для комбинирования иллюстраций и текста в верстке. В композиционной структуре произведений искусства и дизайна имеют значение пропорции прямоугольников и других геометрических фигур, в которые вписывается данное произведение или его основные части. Поэтому следует рассмотреть прямоугольники, которые нашли наиболее широкое применение благодаря своим гармоническим свойствам (о прямоугольнике золотого сечения говорилось выше). Обратимся снова к квадрату. Квадрат как конструктивная форма известен издавна. Он привлекал внимание художников Древнего мира и эпохи Возрождения.

На рисунке Леонардо да Винчи изображена связь квадрата и круга с человеческой фигурой известная еще древним, (Витрувий). Художники Возрождения - немец Дюрер, итальянец Пачоли, француз Тори, занимаясь разработкой начертания букв, исходили из формы квадрата, буква со всеми своими элементами вписывалась в квадрат (рис. 12), хотя и не все буквы приравнивались к квадрату, однако общий композиционный строй определялся квадратом. Квадрат является устойчивой, статичной фигурой. Она ассоциируется с чем_то неподвижным, завершенным. В Древнем мире у некоторых народов изображение квадрата было связано с символикой смерти. (В этой связи интересно заметить, что пропорции квадрата в природе встречаются в формах неживой материи, у кристаллов). Благодаря своей статической завершенности квадрат используется в прикладной графике, в области визуальных коммуникаций наряду с формой круга как элемент, фиксирующий внимание, а также для ограничения пространства, на котором сосредоточена информация.

Помимо прямоугольника золотого сечения и квадрата, наибольший интерес для нас представляют прямоугольники Ц2 и Ц5. Древние греки эпохи классики предпочитали именно эти прямоугольники, Хэмбидж утверждает, что 85% произведений греческого классического искусства построено на пр-ке Ц5. Чем интересен этот прямоугольник? Будучи разделенным по вертикали н по горизонтали на две части, он восстанавливает свои пропорции. Прямоугольник этот можно расчленить на квадрат и два малых прямоугольника золотого сечения. Кроме того, в нем просматриваются два прямоугальника золотого сечения, перекрывающие друг друга на величину квадрата. Оставшаяся часть тоже представляет собой прямоугольник золотого сечения. Таким образом, прямоугольник Ц5 обнаруживает ритмические свойства. В нем возникает красивая симметрия (малый прямоугольник з. с.+ квадрат + малый прямоугольник з. с.).

Рис. 16. Ритмические свойства прямоугольника

Хэмбидж приводит композиционную схему греческой чаши для питья из бостонского музея: чаша вписывается (без ручек) в горизонтально вытянутый прямоугольник Ц5 Диагонали двух прямоугольников золотого сечения, перекрывающих друг друга на квадрат, пересекаются в точке, через которую проходит граница между чашей и ее ножкой. Ширина основания ножки равна высоте чаши и равна стороне квадрата, находящегося в центре прямоугольника Ц5 Ножка вписывается в два малых прямоугольника з. с., отсеченных от квадрата линией, горизонтальной к основанию пр-ка Ц5 и проходящей через точку пересечения двух диагоналей больших прямоугольников з. с. В современном художественном конструировании прямоугольник Ц5 также находит широкое применение. Мы его встречаем в пропорциях автомашин, станков и других изделий. В прикладной графике - в форматах проспектов, буклетов, упаковок; в изобразительном искусстве, в монументальном искусстве, в пропорциях картинной плоскости, в композиционном строе картины.

Прямоугольник Ц2 также находит широкое применение, в осообенности в области прикладной графики. Он используется как формат бумаги для деловой документации, поскольку обладает удивительным свойством, - при делении пополам он не меняет своих пропорций. При делении образуется ряд подобных прямоугольников, гармонически связанных между собой единством формы. На рис. 18 приводится изо6ражение прямоугольников, используемых при композиционном построении благодаря гармоническим отношениям их сторон.

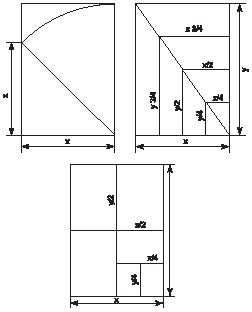
Рис. 17. Пропорции сторон в пр-ке Ц2, использованные в стандарте Поратмана.

Рис. 18. Гармонические отношения сторон в прямоугольниках.

Ниже приводятся числовые отношения пр-ков Ц2, Ц3, Ц4, Ц5 к их обратным числам, с которыми они находятся в гармоническом отношении. (Обратным числом называется число, полученное при делении единицы на данное число). Если принять меньшую сторону прямоугольника за единицу, то для прямоугольника число (соответствующее большей стороне прямоугольника) =1,4142, а обратное число=0,7071; для пр-ка Ц3 число=1,732, обратное число=0,5773; для пр-ка Ц4 число=2, обратноечисло =0,5; для пр-ка Ц5 число=2,236; обратное число=0,4472; для пр-ка" з. с. число= 1,618, обратное число=0,618.

На основе пр-ка Ц2 была проведена стандартизация и унификация форматов книг, бумаг, деловой документации, открыток, плакатов, папок и других объектов, связанных с прикладной графикой. Этот стандарт, известный как стандарт доктора Порстмана был принят в 17 европейских странах. В основу стандарта был положен формат 841Х1189мм и площадью в 1м 2 . От него выведены остальные форматы, составляющие его доли:

1м 2 - 841 Х 1189мм
1/2м 2 - 594 Х841мм
1/4м 2 - 420 Х 594мм
1/8м 2 - 297Х420мм (двойной лист)
1/16м 2 - 210Х 297мм (лист для деловой переписки, бланков)
1/32м 2 - 148Х210мм (пол_листа для деловой переписки, бланков)
1/64м 2 - 105Х148мм (почтовая открытка)
1/128м 2 - 74Х105мм (визитная карточка)

Стандартом предусмотрены и дополнительные форматы 1000Х1414 и 917Х1297 и их доли. Для конвертов предлагаются, размеры: 162Х229 и 114Х162. (Стандарт приведен не полностью).

Рис. 19. Деление прямоугольника на доли: 1/2, 1/4, 1/8, 1/16,1/64.

Поскольку обращение с деловыми бумагами, документацией подразумевает необходимость иметь не только соответствуюшие им по размеру и формату конверты и папки, но и емкости, в которых хранится документация, отсюда возникает необходимость в соответствующей мебели: столах, шкафах, полках. Размеры и пропорции мебели, в свою очередь, подсказывают и характер интерьеров помещений. Таким образом возникает целостная система гармонизованных элементов интерьера, подчиненная единому модульному принципу.

Пропорциональные отношения должны существовать не только между отдельными частями целого, но и между предметами, составляющимигруппы объектов, связанных единым стилем, функциональной задачей. Например, между объектами, входящими в систему фирменного стиля.

Предметы, окружающие человека, должны быть гармонизованы не только по отношению друг к другу, но и связаны с человеком единой мерой, с физическим его строением. Зодчие древности считали, что отношение частей архитектуры друг к другу и к целому должно соответствовать частям человеческого тела, их отношениям. Таким же образом Модулор Корбюзье исходит из размеров человеческого тела и из отношений золотого сечения в нем, (расстояние от земли до солнечного сплетения и расстояние от солнечного сплетения до макушки составляют крайнее и среднее отношения золотого сечения...

Масштабные отношения между вещами, предметным окружением и человеком выступают как средство гармонизации, ибо масштаб является одним из проявлений соразмерности, устанавливающим относительные раамеры между человеком и предметом - в архитектуре, в дизайне, в прикладном искусстве, в частности, в прикладной графике, в искусстве книги. Так, размеры и форматы плакатов и любых объектов, служащих целям визуальной коммуникации - вывесок, дорожных знаков и т. д., а также их композиционное решение всегда избираются в зависимости от назначения и от условий эксплуатацин, а значит и в соответствующих масштабных отношениях. То же самое касается и области книжного оформления и всевозможной печатной рекламы и упаковки.

Симметрия.

В пропорции и соразмерности проявляются количественные отношения между частями целого и целым. Греки к ним присоединяли и симметрию, рассматривая ее как вид соразмерности, - как ее частный случай - тождество. Она, как и пропорция, почиталась необходимым условием гармонии и красоты.

Симметрия основана на подобии. Она означает такое соотношение между элементами, фигурами, когда они повторяют и уравновешивают друг друга. В математике под симметрией подразумевается совмещение частей фигуры при перемещении ее относительно оси или центра симметрии.

Существуют различные виды симметрии. Простейший вид симметрии зеркальная (осевая), возникающая при вращении фигуры вокруг оси симметрии. Симметрия, возникающая при вращении фигуры вокруг центра вращения называется центральной. Наивысшей степенью симметрии обладает шар, так как в центре его пересекается бесконечное множество осей и плоскостей симметрии. Абсолютная, жесткая симметрия характерна для неживой природы - кристаллов (минералов, снежинок).

Для органической природы, для живых организмов характерна неполная симметрия (квазисимметрия), (например, в строении человека). Нарушение симметрии, асимметрия (отсутствие симметрии) используется в искусстве как художественное средство. Небольшое отклонение от правильной симметрии, то есть некоторая асимметричность, нарушая равновесие, привлекает к себе внимание, вносит элемент движения и создает впечатление живой формы. Различные виды симметрии обладают различным воздействием на эстетическое чувство:

зеркальная симметрия - равновесие, покой;
винтовая симметрия вызывает ощущение движения...

Хзмбидж причисляет все простые геометрические фигуры к статичной симметрии, (разделяя все виды симметрии на статичные и динамичные), а к динамичной симметрии относит спираль. В основе статичной симметрии часто лежит пятиугольник (срез цветка или плода) или квадрат (в минералах). В искусстве строгая математическая симметрия используется редко.

Рис. 20. Виды симметрии: Зеркальная, винтовая, центральная, по сдвигу.

Рис. 21. "Линия грации и красоты" Хогарта

Симметрия связана с понятием середины и целого. В древнегреческой философии и искусстве понятие "середины, центра связано с представлением о цельности бытия". Середина - "избегание крайностей" (Аристотель) - означает принцип уравновешенности. "Везде грек видел нечто цельное. А это и значит, что он прежде всего фиксировал центр набпюдаемого или постороннего предмета... Без понятия "середины" немыслимо античное учение о пропорциях, мере, симметрии или гармонии".

Гармония

Гармония - понятие диалектическое. По древнегреческой мифологии Гармония - дочь бога войны Арея и богини любви и красоты Афродиты, то есть, в ней слиты противоположные, враждующие начала. Поэтому понятие гармонии включает в себя контраст как необходимое условие. Контраст способствует многообразию и разнообразию, без которых немыслима гармония.

"Гармония есть единение многого и согласие несогласного " (Филолай). Это знали древние. Художник XVIII в. Хогарт находил, что сущностьгармонии в единстве и разнообразии. Он преклонялся перед волнообразной линией, которую считал "линией красоты и грации ", потому что она является конкретным воплощением единства и разнообразия. Без разнообразия невозможна красота. Однообразие утомляет. В смене противоположного проявляется диалектическая закономерность - отрицание отрицания. В зримых образах искусства она выражается через ритм и контраст. Смысл гармонии в обуздании хаоса.

Но она осуществляет это через борьбу противоположных начал. Объединяя противоположные начала, гармония уравновешивает их, вносит меру и согласие, упорядочивает и в награду получает красоту.

Симметрия, пропорции, ритм, контраст, цельность - образующие гармонию объективно связаны с природой, с движением и развитием материи. Наши эстетические представления тесно связаны с этими понятиями. Однако, социальное бытие человека в разные эпохи под разным углом зрения рассматривало категории гармонии и это определяло их роль в общественной жизни и в искусстре. Представление о прекрасном развивалось, менялось. Гармония стала рассматриваться не как количественный, а как качественный принцип, объединяя физическое и духовное начала.

Если древние греки считали прекрасным только упорядоченное и всякое нарушение симметрии и пропорций находили безобразным, то в последующие эпохи проявления прекрасного стали обнаруживать и в нарушении порядка, в диссонансах, в кажущейся дисгармонии, ибо они свойственны жизни и, следовательно, являются частью какой_то иной гармонической системы, в которой обретают логику и смысл. "Прекрасное - есть жизнь", писал Чернышевский. И она не стоит на месте. Появления гармонии в природе и жизни шире, чем это может охватить любой канон, любая гармоническая система. И человечество никогда не перестанет искать новых гармонических отношений, сочетаний, искать проявления иных гермонических закономерностей. Однако, это не значит, что классическая гармония потеряла свое значение. То, что уже открыто, те найденные закономерности, их математическое обоснование, остаются вечным достоянием человечества, из которого будут черпать все последующие поколения.

перейти к следующей части - " "

Если внимательно посмотреть по сторонам, роль математики в жизни человека становится очевидной. Компьютеры, современные телефоны и прочая техника сопровождают нас каждый день, а их создание невозможно без использования законов и расчетов великой науки. Однако роль математики в и общества не исчерпывается подобным ее применением. Иначе, например, многие деятели искусства могли бы с чистой совестью сказать, что время, посвященное в школе решению задач и доказательству теорем, было потрачено впустую. Тем не менее это не так. Попробуем разобраться, для чего нужна математика.

Основание

Для начала стоит понять, что вообще представляет собой математика. В переводе с древнегреческого само ее название означает «наука», «изучение». В основе математики лежат операции подсчета, измерения и описания форм объектов. на который опираются знания о структуре, порядке и отношениях. Именно они составляют суть науки. Свойства реальных объектов в ней идеализируются и записываются на формальном языке. Так происходит их преобразование в математические объекты. Часть идеализированных свойств становятся аксиомами (утверждениями, не требующими доказательств). Из них затем выводятся другие истинные свойства. Так формируется реально существующего объекта.

Два раздела

Математику можно разделить на две взаимодополняющие части. Теоретическая наука занимается глубоким анализом внутриматематических структур. Прикладная же предоставляет свои модели другим дисциплинам. Физика, химия и астрономия, инженерные системы, прогнозирование и логика используют математический аппарат постоянно. С его помощью делаются открытия, обнаруживаются закономерности, предугадываются события. В этом смысле значение математики в жизни человека невозможно переоценить.

Основа профессиональной деятельности

Без знания основных математических законов и умения ими пользоваться в современном мире становится очень трудно обучаться практически любым профессиям. С цифрами и операциями с ними имеют дело не только финансисты и бухгалтера. Астроном не сможет определить без таких знаний расстояние до звезды и наилучшее время наблюдения за ней, а молекулярный биолог — понять, как бороться с генной мутацией. Инженер не сконструирует рабочую систему сигнализации или видеонаблюдения, а программист не найдет подход к операционной системе. Многие из этих и других профессий без математики просто не существуют.

Гуманитарные знания

Однако не столь очевидна роль математики в жизни человека, например, посвятившего себя живописи или литературе. И все же следы царицы наук присутствуют и в гуманитарных знаниях.

Казалось бы, поэзия — сплошная романтика и вдохновение, в ней нет места анализу и расчету. Однако достаточно вспомнить стихотворные размеры амфибрахий), как приходит понимание, что математика и тут приложила свою руку. Ритм, словесный или музыкальный, также описывается и просчитывается с применением знаний этой науки.

Для писателя или психолога часто важны такие понятия, как достоверность информации, единичный случай, обобщение и так далее. Все они либо напрямую являются математическими, либо строятся на основе закономерностей, разработанных царицей наук, существуют благодаря ей и по ее правилам.

Психология родилась на стыке гуманитарных и естественных наук. Все ее направления, даже те, что работают исключительно с образами, опираются на наблюдение, анализ данных, их обобщение и верификацию. Здесь используется и моделирование, и прогнозирование, и статистические методы.

Со школы

Математика в нашей жизни присутствует не только в процессе освоения профессии и реализации полученных знаний. Так или иначе мы используем царицу наук практически в каждый момент времени. Именно поэтому математике начинают обучать достаточно рано. Решая простые и сложные задачи, ребенок не просто учится складывать, вычитать и умножать. Он медленно, с азов постигает устройство современного мира. И речь тут идет не о техническом прогрессе или умении проверять сдачу в магазине. Математика формирует некоторые особенности мышления и оказывает влияние на отношение к миру.

Самое простое, самое сложное, самое главное

Наверное, все вспомнят хотя бы один вечер за домашним заданием, когда хотелось отчаянно взвыть: «Я не понимаю, для чего нужна математика!», отбросить в сторону ненавистные сложные и нудные задачки и сбежать во двор к друзьям. В школе и даже позже, в институте, заверения родителей и преподавателей «потом пригодится» кажутся надоедливым бредом. Однако они, оказывается, правы.

Именно математика, а затем и физика, учит находить причинно-следственные связи, закладывает привычку искать пресловутое «откуда ноги растут». Внимание, сосредоточенность, сила воли — они также тренируются в процессе решения тех самых ненавистных задачек. Если пойти дальше, то умение выводить следствия из фактов, прогнозировать будущие события, а также делать тоже закладываются во время изучения математических теорий. Моделирование, абстрагирование, дедукция и индукция — все это наук и одновременно способы работы мозга с информацией.

И снова психология

Часто именно математика дарит ребенку откровение, что взрослые не всемогущи и знают далеко не все. Так бывает, когда мама или папа на просьбу помочь решить задачку лишь разводят руками и объявляют о своей неспособности это сделать. И ребенок вынужден сам искать ответ, ошибаться и снова искать. Бывает и так, что родители просто отказываются помочь. «Ты должен сам», — говорят они. И правильно делают. После многочасовых попыток ребенок получит не просто сделанное домашнее задание, но способность самостоятельно находить решения, обнаруживать и исправлять ошибки. И в этом также кроется роль математики в жизни человека.

Конечно, самостоятельность, умение принимать решения, отвечать за них, отсутствие страха перед ошибками вырабатываются не только на уроках алгебры и геометрии. Но эти дисциплины играют в процессе немалую роль. Математика воспитывает такие качества, как целеустремленность и активность. Правда, многое зависит и от учителя. Неправильная подача материала, излишняя строгость и давление могут, наоборот, привить страх перед трудностями и ошибками (сначала на уроках, а потом и в жизни), нежелание высказывать свое мнение, пассивность.

Математика в повседневной жизни

Взрослые люди после окончания университета или колледжа не перестают каждый день решать математические задачи. Как успеть на поезд? Получится ли из килограмма мяса приготовить ужин для десяти гостей? Сколько калорий в блюде? На какое время хватит одной лампочки? Эти и многие другие вопросы имеют прямое отношение к царице наук и без нее не решаются. Получается, математика в нашей жизни незримо присутствует практически постоянно. Причем чаще всего мы этого даже не замечаем.

Математика в жизни общества и отдельного человека затрагивает огромное количество областей. Некоторые профессии без нее немыслимы, многие появились только благодаря развитию отдельных ее направлений. Современный технический прогресс тесно связан с усложнением и развитием математического аппарата. Компьютеры и телефоны, самолеты и космические аппараты никогда бы не появились, не будь людям известна царица наук. Однако роль математики в жизни человека этим не исчерпывается. Наука помогает ребенку осваивать мир, обучает более эффективному взаимодействию с ним, формирует мышление и отдельные качества характера. Впрочем, сама по себе математика не справилась бы с такими задачами. Как было сказано выше, огромную роль играет подача материала и особенности личности того, кто знакомит ребенка с миром.

В заключение мы попытаемся в кратких чертах охарактеризовать общие закономерности развития математики.

1. Математика не есть создание какой-либо одной исторической эпохи, какого-либо одного народа; она есть продукт ряда эпох, продукт работы многих поколений. Ее первые понятия и положения возникли,

как мы видели, в глубокой древности и уже более двух тысяч лет назад были приведены в стройную систему. Несмотря на все преобразования математики, ее понятия и выводы сохраняются, переходя из одной эпохи к другой, как, например, правила арифметики или теорема Пифагора.

Новые теории включают в себя предшествующие достижения, уточняя, дополняя и обобщая их.

В то же время, как ясно из данного выше краткого очерка истории математики, ее развитие не только не сводится к простому накоплению новых теорем, но включает существенные, качественные изменения. Соответственно, развитие математики разделяется на ряд периодов, переходы между которыми как раз и обозначены такими коренными изменениями в самом предмете или структуре этой науки.

Математика включает в свою сферу все новые области количественных отношений действительности. В то же время важнейшим предметом математики были и остаются пространственные формы и количественные отношения в простом, наиболее непосредственном смысле этих слов, и математическое осмысление новых связей и отношений неминуемо происходит на основе и в связи с уже сложившейся системой количественных и пространственных научных представлений.

Наконец, накопление результатов внутри самой математики необходимо влечет как восхождение к новым ступеням абстракции, к новым обобщающим понятиям, так и углубление в анализ основ и первоначальных понятий.

Как дуб в своем могучем росте утолщает Старые ветви новыми слоями, выбрасывает новые ветви, тянется вверх и углубляется корнями вниз, так и математика в своем развитии накапливает новый материал в уже сложившихся своих областях, образует новые направления, восходит к новым вершинам абстракции и углубляется в своих основах.

2. Математика имеет своим предметом реальные формы и отношения действительности, но, как говорил Энгельс, чтобы изучить эти формы и отношения в чистом виде, необходимо совершенно отделить их от их содержания, оставить это последнее в стороне как нечто безразличное. Однако форм и отношений вне содержания не существует, математические формы и отношения не могут быть абсолютно безразличными к содержанию. Стало быть, математика, по самой своей сущности стремящаяся осуществить такое отделение, стремится осуществить невозможное. Это и есть коренное противоречие в самой сущности математики. Оно является специфическим для математики проявлением общего противоречия познания. Отображение мыслью всякого явления, всякой стороны, всякого момента действительности огрубляет, упрощает его, выхватывая его из общей связи природы. Когда люди, изучая свойства пространства, установили, что оно имеет эвклидову геометрию, был совершен исключительно

важный акт познания, но в нем же заключалось заблуждение: реальные свойства пространства были [взяты упрощенно, схематично, в отвлечении от материи. Но без этого просто не было бы геометрии, и именно на почве этого отвлечения (как из внутреннего его исследования, так и из сопоставления математических результатов с новыми данными других наук) зарождались и укреплялись новые геометрические теории.

Постоянное разрешение и восстановление указанного противоречия на все более приближающихся к действительности ступенях познания и составляет сущность развития познания. При этом определяющим является, конечно, положительное содержание познания, элемент абсолютной истины в нем. Познание идет по восходящей линии, а не топчется на месте в простом смешении с заблуждением. Движение познания есть постоянное преодоление его неточности и ограниченности.

Указанное основное противоречие влечет за собой другие. Мы видели это на примере противоположностей дискретного и непрерывного. (В природе между ними нет абсолютного разрыва, и их разделение в математике неизбежно влекло необходимость создания все новых понятий, глубже отражающих действительность и одновременно преодолевающих внутренние несовершенства существующей математической теории). Совершенно так же противоречия конечного и бесконечного, абстрактного и конкретного, формы и содержания и др. выступают в математике как проявления ее коренного противоречия. Но решающее его проявление состоит в том, что, отвлекаясь от конкретного, вращаясь в кругу своих абстрактных понятий, математика тем самым отделяется от эксперимента и практики, а вместе с тем она лишь постольку является наукой (т. е. имеет познавательную ценность), поскольку опирается на практику, поскольку оказывается не чистой, а прикладной математикой. Говоря несколько гегелевским языком, чистая математика постоянно «отрицает» себя как чистую математику, без этого она не может иметь научного значения, не может развиваться, не может преодолевать неминуемо возникающие внутри нее трудности.

В своем формальном виде математические теории противостоят реальному содержанию как некоторые схемы для конкретных выводов. Математика выступает при этом как метод формулировки количественных законов естествознания, как аппарат для разработки его теорий, как средство решения задач естествознания и техники. Значение чистой математики на современном этапе заключено прежде всего в математическом методе. И как всякий метод существует и развивается не сам по себе, а только на основе своих применений, в связи с содержанием, к которому он применяется, так и математика не может существовать и развиваться без применений. Здесь опять обнаруживается единство противоположностей: общий метод противостоит конкретной задаче, как средство ее решения, но он сам возникает из обобщения конкретного материала и существует

развивается и находит свое оправдание только в решении конкретных задач.

3. Общественная практика играет определяющую роль в развитии математики в трех отношениях. Она ставит перед математикой новые проблемы, стимулирует ее развитие в том или ином направлении и дает критерий истинности ее выводов.

Это чрезвычайно ясно видно на примере возникновения анализа. Во-первых, именно развитие механики и техники выдвинуло проблему изучения зависимостей переменных величин в их общем виде. Архимед, подойдя вплотную к дифференциальному и интегральному исчислению, оставался, однако, в рамках задач статики, тогда как в новое время имен но исследование движения породило понятия переменной и функции и понудило к оформлению анализа. Ньютон не мог развить механику, не развивая соответствующего математического метода.

Во-вторых, именно потребности общественного производства побуждали к постановке и решению всех этих проблем. Ни в античном, ни в средневековом обществе этих стимулов еще не было. Наконец, весьма характерно, что математический анализ в своем возникновении находил обоснование своих выводов именно в приложениях. Только поэтому он и мог развиваться без тех строгих определений его основных понятий (переменная, функция, предел), которые были даны позже. Истинность анализа устанавливалась применениями в механике, физике и технике.

Сказанное относится ко всем периодам развития математики. Начиная с XVII в. наиболее непосредственное влияние на ее развитие оказывают вместе с механикой теоретическая физика и проблемы новой техники. Механика сплошной среды, а потом теория поля (теплопроводность, электричество, магнетизм, поле тяготения) направляют развитие теории дифференциальных уравнений в частных производных. Разработка молекулярной теории и вообще статистической физики, начиная с конца прошлого века, служила важным стимулом развития теории вероятностей, особенно теории случайных процессов. Теория относительности сыграла решающую роль в развитии римановой геометрии с ее аналитическими методами и обобщениями.

В настоящее время развитие новых математических теорий, как функциональный анализ и др., стимулируется проблемами квантовой механики и электродинамики, задачами вычислительной техники, статистическими вопросами физики и техники и т. д. и т. п. Физика и техника не только ставят перед математикой новые задачи, наталкивают ее на новые предметы исследования, но также пробуждают развитие нужных для них разделов математики, которые складывались первоначально в большей мере внутри нее самой, как это было с римановой геометрией. Короче, для интенсивного развития науки нужно, чтобы она не только подошла к решению новых задач, но чтобы необходимость их решения навязывалась

потребностями развития общества. В математике в последнее время возникает много теорий, но только те из них получают развитие и прочно входят в науку, которые нашли свои применения в естествознании и технике либо сыграли роль важных обобщений тех теорий, которые имеют такие приложения. Вместе с тем другие теории остаются без движения, как, например, некоторые рафинированные геометрические теории (недезарговы, неархимедовы геометрии), не нашедшие существенных применений.

Истинность математических выводов находит свое последнее основание не в общих определениях и аксиомах, не в формальной строгости доказательств, а в реальных приложениях, т. е. в конечном счете в практике.

В целом, развитие математики нужно понимать прежде всего как результат взаимодействия логики ее предмета, отраженной во внутренней логике самой математики, влияния производства и связей с естествознанием. Это различие идет сложными путями борьбы противоположностей, включая существенные изменения в основном содержании и формах математики. По содержанию развитие математики определяется ее предметом, но побуждается оно в основном и в конечном счете потребностями производства. Такова основная закономерность развития математики.

Конечно, мы не должны забывать при этом, что речь идет лишь об основной закономерности и что связь математики с производством, вообще говоря, является сложной. Из того, что говорилось выше, ясно, что было бы наивным пытаться обосновать появление каждой данной математической теории непосредственным «производственным заказом». Более того, математика, как и всякая наука, обладает относительной самостоятельностью, своей внутренней логикой, отражающей, как мы это подчеркивали, объективную логику, т. е. закономерность ее предмета.

4. Математика всегда испытывала самое существенное влияние не только общественного производства, но и всех общественных условий в целом. Ее блестящий прогресс в эпоху возвышения древней Греции, успехи алгебры в Италии в эпоху Возрождения, развитие анализа в эпоху, последовавшую за английской революцией, успехи математики во Франции в период, примыкающий к Французской революции, - все это убедительно демонстрирует неразрывную связь прогресса математики с общим техническим, культурным, политическим прогрессом общества.

Это также ярко видно на примере развития математики в России. Становление самостоятельной русской математической школы, идущей от Лобачевского, Остроградского и Чебышева, нельзя отделить от прогресса русского общества в целом. Время Лобачевского - это время Пушкина,

Глинки, время декабристов, и расцвет математики был одним из элементов общего подъема.

Тем более убедительно влияние общественного развития в период после Великой Октябрьской социалистической революции, когда исследования фундаментального значения появлялись друг за другом с поразительной быстротой во многих направлениях: в теории множеств, топологии, теории чисел, теории вероятностей, теории дифференциальных уравнений, функциональном анализе, алгебре, геометрии.

Наконец, математика всегда испытывала и испытывает на себе заметное влияние идеологии. Как и во всякой науке, объективное содержание математики воспринимается и толкуется математиками и философами в рамках той или иной идеологии.

Короче, объективное содержание науки всегда укладывается в те или иные идеологические формы; единство и борьба этих диалектических противоположностей - объективного содержания и идеологических форм - в математике, как и во всякой науке, играют далеко не последнюю роль в ее развитии.

Борьба материализма, отвечающего объективному содержанию науки, с идеализмом, противоречащим этому содержанию и извращающим его понимание, идет через всю историю математики. Эта борьба ясно обозначена уже в древней Греции, где против материализма Фалеса, Демокрита и других философов, создававших греческую математику, выступал идеализм Пифагора, Сократа и Платона. С развитием рабовладельческого строя верхушка общества отрывалась от участия в производстве, считая его уделом низшего класса, и это порождало отрыв «чистой» науки от практики. Достойной внимания истинного философа признавалась лишь чисто теоретическая геометрия. Характерно, что появившиеся исследования некоторых механических кривых и даже конических сечений Платон считал остающимися за пределами геометрии, так как они «не приводят нас в общение с вечными и бестелесными идеями» и «нуждаются в применении орудий пошлого ремесла».

Яркий пример борьбы материализма против идеализма в математике представляет деятельность Лобачевского, который выдвинул и отстаивал материалистическое понимание математики против идеалистических взглядов кантианства.

Для русской математической школы вообще характерна материалистическая традиция. Так, Чебышев явно подчеркивал решающее значение практики, а Ляпунов выразил стиль отечественной математической школы в следующих замечательных словах: «Детальная разработка вопросов, особенно важных сточки зрения приложения и в то же время представляющих особенные теоретические трудности, требующие изобретения новых методов и восхождения к принципам науки, затем обобщение полученных выводов и создание этим путем более или менее общей теории». Обобщения и абстракции не сами по себе, а в связи с конкретным материалом

теоремы и теории не сами по себе, а в общей связи науки, ведущей в конечном счете к практике, - вот что оказывается на самом деле важным и перспективным.

Таковы же были устремления таких великих ученых, как Гаусс и Риман.

Однако с развитием капитализма в Европе материалистические взгляды, отражавшие передовую идеологию возвышающейся буржуазии эпохи XVI - начала XIX вв., стали сменяться идеалистическими воззрениями. Так, например, Кантор (1846-1918), создавая теорию бесконечных множеств, прямо ссылался на бога, высказываясь в том духе, что бесконечные множества имеют абсолютное существование в божественном разуме. Крупнейший французский математик конца XIX- начала XX в. Пуанкаре выдвинул идеалистическую концепцию «конвенционализма», согласно которой математика есть схема условных соглашений, принимаемых для удобства описания многообразия опыта. Так, по мнению Пуанкаре, аксиомы эвклидовой геометрии суть не более как условные соглашения и значение их определяется удобством и простотой, но не соответствием реальной действительности. Поэтому Пуанкаре говорил, что, например, в физике скорее откажутся от закона прямолинейного распространения света, чем от эвклидовой геометрии. Эта точка зрения была опровергнута развитием теории относительности, которая, вопреки всей «простоте» и «удобству» эвклидовой геометрии, в полном согласии с материалистическими идеями Лобачевского и Римана, привела к выводу, что реальная геометрия пространства отлична от эвклидовой.

На почве трудностей, возникших в теории множеств, и в связи с необходимостью анализа основных понятий математики, среди математиков в начале XX в. появились разные течения. Единство в понимании содержания математики было утрачено; разные математики стали по-разному рассматривать не только общие основы науки, что было и раньше, но даже по-разному стали оценивать смысл и значение отдельных конкретных результатов и доказательств. Выводы, казавшиеся осмысленными и содержательными для одних, другие объявляли лишенными смысла и значения. Возникли идеалистические течения «логицизма», «интуиционизма» «формализма» и др.

Логисты утверждают, что вся математика выводима из понятий логики. Интуиционисты видят источник математики в интуиции и придают смысл лишь интуитивно воспринимаемому. Поэтому они, в частности, вовсе отрицают значение канторовской теории бесконечных множеств. Более того, интуиционисты отрицают простой смысл даже таких утверждений

как теорема о том, что всякое алгебраическое уравнение степени имеет корней. Для них это утверждение пусто, пока не указан способ вычисления корней. Так, полное отрицание объективного смысла математики привело интуиционистов к опорочиванию, как «лишенной смысла», значительной части достижений математики. Наиболее крайние из них дошли до утверждения, что существует столько математик, сколько есть математиков.

Попытку по-своему спасти математику от такого рода нападок предпринял крупнейший математик начала нашего века - Д. Гильберт. Сущность его идеи сводилась к тому, чтобы свести математические теории к чисто формальным операциям над символами согласно предписанным правилам. Расчет состоял в том, что при таком совершенно формальном подходе все трудности будут сняты, ибо предметом математики окажутся символы и правила действия с ними без всякого отношения к их смыслу. Это и есть установка формализма в математике. По словам интуициониста Брауэра, для формалиста истина математики на бумаге, тогда как для интуициониста она в голове математика.

Нетрудно, впрочем, видеть, что оба они неправы, ибо математика, а вместе с тем и то, что написано на бумаге, и то, что думает математик, отражает действительность, и истина математики заключается в ее соответствии объективной действительности. Отрывая математику от материальной действительности, все эти течения оказываются идеалистическими.

Идея Гильберта потерпела поражение в результате ее собственного развития. Австрийский математик Гедель доказал, что даже арифметику нельзя формализовать полностью, как на то рассчитывал Гильберт. Вывод Геделя явно вскрыл внутреннюю диалектику математики, которая не позволяет исчерпать ни одну ее область формальным исчислением. Даже простейшая бесконечность натурального ряда чисел оказалась неисчерпываемой конечной схемой символов и правил действия с ними. Так, было математически доказано то, что высказал в общем виде еще Энгельс, когда писал:

«Бесконечность есть противоречие... Уничтожение этого противоречия было бы концом бесконечности». Гильберт рассчитывал заключить математическую бесконечность в рамки конечных схем и тем самым ликвидировать все противоречия и трудности. Это оказалось невозможным.

Но в условиях капитализма конвенционализм, интуиционизм, формализм и другие подобные течения не только сохраняются, ной дополняются новыми вариантами идеалистических взглядов на математику. Теории, связанные с логическим анализом основ математики, существенно используются в некоторых новых вариантах субъективного идеализма. Субъективный

идеализм использует теперь математику, в частности математическую логику, не меньше, чем физику, и потому вопросы понимания основ математики приобретают особую остроту.

Так, трудности развития математики породили в условиях капитализма идеологический кризис этой науки, сходный в своих основах с кризисом физики, сущность которого была выяснена Лениным в его гениальном произведении «Материализм и эмпириокритицизм». Этот кризис вовсе не означает, что математика в капиталистических странах совершенно задержана в своем развитии. Ряд ученых, стоящих на явно идеалистических позициях, делает важные, порой выдающиеся успехи в решении конкретных математических вопросов и развитии новых теорий. Достаточно сослаться на блестящую разработку математической логики.

Коренной порок распространенного в капиталистических странах взгляда на математику состоит в его идеализме и метафизике: в отрыве математики от действительности и пренебрежении ее реальным развитием. Логистика, интуиционизм, формализм и другие подобные направления выделяют в математике какую-нибудь одну ее сторону - связь с логикой, интуитивную ясность, формальную строгость и т. п. - неосновательно преувеличивают, абсолютизируют ее значение, отрывают ее от действительности и за глубоким анализом этой одной черты математики самой по себе теряют из виду математику в целом. Именно вследствие этой односторонности ни одно из этих течений при всей тонкости и глубине отдельных выводов не может привести к верному пониманию математики. В противоположность различным течениям и оттенкам идеализма и метафизики диалектический материализм рассматривает математику, как и всю науку в целом, такой, как она есть, во всем богатстве и сложности ее связей и развития. И именно потому, что диалектический материализм стремится понять все богатство и всю сложность связей науки с действительностью, всю сложность ее развития, идущего от простого обобщения опыта к высшим абстракциям и от них к практике, именно потому, что самый свой подход к науке он постоянно приводит в соответствие с ее объективным содержанием, с ее новыми открытиями, именно поэтому и, в конечном счете только поэтому, он и оказывается единственной подлинно научной философией, ведущей к верному пониманию науки вообще и, в частности, - математики.